Unlock The Mystery: 20 Is What Percent Of 50?
Understanding percentages is a fundamental skill that permeates countless aspects of our daily lives, from calculating discounts during a sale to interpreting financial reports or even understanding statistics in the news. The question "20 is what percent of 50?" might seem like a simple mathematical puzzle, but mastering this concept unlocks a deeper comprehension of proportional relationships, a cornerstone of numerical literacy. This article will demystify percentages, providing a clear, step-by-step guide to solving this common problem and equipping you with the knowledge to tackle similar calculations with confidence.
Whether you're a student grappling with math homework, a consumer trying to make informed purchasing decisions, or simply someone looking to sharpen their quantitative skills, grasping the essence of percentages is invaluable. We'll explore the underlying principles, practical applications, and common pitfalls, ensuring that by the end of this comprehensive guide, you'll not only know the answer to "20 is what percent of 50?" but also understand the 'why' and 'how' behind it, empowering you to apply this knowledge effectively in various real-world scenarios.
Table of Contents
- Understanding the Basics of Percentages
- Why Do Percentages Matter?
- The Formula Unveiled: How to Calculate Percentages
- Common Misconceptions and How to Avoid Them
- Practical Applications of Percentage Calculations
- The Evolution of Mathematical Tools and Precision
- Beyond the Basics: Advanced Percentage Concepts
- Mastering Numerical Literacy: A Lifelong Skill
Understanding the Basics of Percentages
At its core, a percentage is simply a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" or "out of one hundred." This makes it an incredibly intuitive and standardized way to compare different quantities or proportions, regardless of their original scale. When we say 50%, we mean 50 out of 100, or 1/2. When we ask "20 is what percent of 50?", we are essentially asking: if 50 represents the whole (or 100%), what proportion of that whole is 20, expressed in terms of a hundred? Think of it like a pie chart divided into 100 slices. If you have 20 slices out of a total of 50 slices in a different pie, how many slices would that be if the pie had 100 slices in total? The beauty of percentages lies in their ability to normalize comparisons. Whether you're comparing a small part of a small number or a large part of a large number, converting them to a percentage provides a common ground for understanding their relative size. This standardization is crucial in many fields, from academic research to business analytics, allowing for clear and unambiguous communication of proportional data. It’s a concept so fundamental that it often appears in early mathematical education, laying the groundwork for more complex statistical and financial analyses.Why Do Percentages Matter?
The relevance of percentages extends far beyond the classroom. They are a universal language for expressing proportions, making them indispensable in almost every facet of modern life. In finance, interest rates, stock market gains or losses, and inflation figures are all expressed as percentages. In retail, discounts and sales tax are percentage-based. Health and science rely on percentages to report data, such as success rates of treatments or the composition of substances. Even in everyday conversations, we often use percentages to convey a sense of scale or likelihood – "I'm 90% sure," or "The project is 75% complete." Consider the "Data Kalimat" provided, where someone mentions "147k 20 20 gold badges 177 177 silver badges 287 287 bronze badges." While these are counts, imagine if we wanted to know what percentage of all badges were gold, silver, or bronze. Percentages would immediately give us a clearer picture of the distribution of these achievements. Similarly, when discussing software versions like "versions 23.10.0 and 16.20.2" or "Microsoft added the possibility of downloading media in version 2022," understanding the percentage of users on a particular version, or the percentage of new features in an update, provides valuable context. Percentages empower us to make informed decisions, critically evaluate information, and communicate numerical insights effectively, solidifying their status as a vital component of numerical literacy.The Formula Unveiled: How to Calculate Percentages
Calculating a percentage involves a straightforward formula. To find out what percentage one number (the part) is of another number (the whole), you simply divide the part by the whole and then multiply the result by 100. The general formula is: **Percentage = (Part / Whole) × 100** Let's break down the components: * **Part:** This is the specific quantity or amount you are interested in expressing as a percentage. In our core question, "20 is what percent of 50?", the 'part' is 20. * **Whole:** This is the total quantity, the base amount against which the part is being compared. In our question, the 'whole' is 50. * **× 100:** Multiplying by 100 converts the decimal or fractional result into a percentage, expressing it "per hundred." This formula is universally applicable, whether you're calculating a test score, determining the proportion of a budget spent on a particular category, or answering the question "20 is what percent of 50?". It provides a consistent method for translating raw numbers into a comparative percentage format, making complex data more accessible and understandable.Step-by-Step: Solving "20 is What Percent of 50?"
Let's apply the formula directly to our central question: "20 is what percent of 50?" 1. **Identify the Part and the Whole:** * The part is 20. * The whole is 50. 2. **Divide the Part by the Whole:** * 20 ÷ 50 = 0.4 3. **Multiply the Result by 100:** * 0.4 × 100 = 40 4. **Add the Percentage Symbol:** * 40% Therefore, **20 is 40% of 50**. It's as simple as that! This methodical approach ensures accuracy and can be applied to any similar percentage problem. The key is correctly identifying which number represents the 'part' and which represents the 'whole'. This calculation is fundamental and serves as a building block for more complex percentage problems you might encounter in various real-world scenarios, from financial planning to academic performance evaluations. The clarity and simplicity of this method make it a cornerstone of basic quantitative reasoning.Common Misconceptions and How to Avoid Them
While calculating percentages seems straightforward, several common misconceptions can lead to errors. One frequent mistake is confusing the 'part' and the 'whole', or incorrectly identifying which number should be the numerator and which the denominator. For instance, if you wanted to find what percent 50 is of 20, the calculation would be 50/20 * 100 = 250%, a very different result from 40%. Always ask yourself: "What quantity am I comparing *to* what total?" Another pitfall is forgetting to multiply by 100, leaving the answer as a decimal or fraction. While 0.4 is mathematically equivalent to 40%, expressing it as 0.4 does not answer the question "what percent?" The percentage symbol (%) specifically denotes "per hundred." Furthermore, when dealing with percentage increases or decreases, people sometimes use the wrong base number. For example, if a price increases from $20 to $25, the increase is $5. The percentage increase is ($5 / $20) * 100 = 25%, not ($5 / $25) * 100 = 20%. The base (the 'whole') for an increase is the *original* amount. The "Data Kalimat" provides an interesting analogy for precision: "As the aforementioned rfc does not include any reference of encoding spaces as +, i guess using %20 is the way to go today,I am just trying to." This highlights the importance of adhering to established standards and conventions for accuracy, whether in technical encoding or mathematical calculations. Just as using "%20" for spaces ensures correct interpretation in web addresses, using the correct formula and base number ensures accurate percentage calculations. Double-checking your numbers and understanding the context of the problem are key to avoiding these common errors and ensuring your results are reliable.Practical Applications of Percentage Calculations
The ability to calculate percentages is not just an academic exercise; it's a vital life skill with extensive practical applications across various domains. From managing personal finances to understanding global economic trends, percentages provide a standardized way to interpret and compare data.Finance and Investments
In the world of finance, percentages are ubiquitous. Interest rates on loans and savings accounts are expressed as percentages. Investment returns, whether from stocks, bonds, or mutual funds, are typically reported as percentage gains or losses. Understanding "20 is what percent of 50" helps build the foundation for more complex financial calculations, such as calculating compound interest or understanding the percentage yield of a dividend. When you see an advertisement for a credit card with an Annual Percentage Rate (APR), your ability to grasp what that percentage means for your total repayment is crucial for financial well-being. Similarly, inflation rates, which measure the percentage increase in the price of goods and services over time, directly impact purchasing power and are essential for economic planning. The snippet from the "Data Kalimat" about "i don't want to spend a penny with it, so i got myself a free host" reflects a common financial decision-making process: seeking cost-effective solutions. Calculating the percentage savings achieved by opting for a free service versus a paid one is a direct application of percentage understanding, enabling smarter financial choices.Everyday Consumer Decisions
Beyond finance, percentages empower consumers to make smarter choices. Sales and discounts are almost always advertised as percentages off the original price. Knowing how to calculate "20% off" or "30% discount" allows you to quickly determine the final price and compare deals. Sales tax, tips at restaurants, and even nutritional information on food labels (e.g., "Daily Value %") all rely on percentage calculations. For example, if a product originally costs $50 and is on sale for 20% off, you can quickly calculate that the discount is $10 (20% of $50), making the final price $40. This is directly related to our core question, reinforcing how "20 is what percent of 50" translates into real-world scenarios. Understanding these calculations helps you budget effectively, avoid overspending, and ensure you're getting the best value for your money.The Evolution of Mathematical Tools and Precision
The way we approach and execute calculations has evolved significantly over time, mirroring advancements in technology and our understanding of efficiency. Historically, complex percentage calculations might have required manual methods, perhaps using pen and paper or even abacuses. Today, we have calculators, spreadsheets, and sophisticated software that can perform these operations instantly and with high precision. The "Data Kalimat" offers an interesting glimpse into this evolution with mentions of "check your node version," "versions 23.10.0 and 16.20.2," and "Microsoft added the possibility of downloading media in version 2022." These snippets illustrate how technology iterates and improves, providing newer, often more efficient "versions" of tools. Just as software development progresses, our methods for mathematical problem-solving also become more refined. If you need an older version and can't apply juki's answer, you can use fiddler to" suggests that sometimes, understanding foundational principles (like the core percentage formula) is crucial, even when advanced tools are available, especially if you need to troubleshoot or work with legacy systems. The importance of precision is also subtly highlighted. While for "20 is what percent of 50" the answer is a clean 40%, many real-world percentage calculations involve decimals that require careful rounding or full precision. The need for accurate tools and methods ensures that financial reports, scientific data, and consumer information are reliable. The shift from manual computation to digital tools underscores a broader trend towards efficiency and accuracy in all quantitative fields, making numerical literacy more accessible yet also demanding a foundational understanding to interpret results correctly.Beyond the Basics: Advanced Percentage Concepts
Once you've mastered the fundamental calculation of "20 is what percent of 50," you can easily progress to more advanced percentage concepts that are frequently encountered in business, economics, and data analysis. These include percentage increase/decrease, percentage points, and inverse percentage problems.Percentage Increase and Decrease
Calculating percentage increase or decrease is crucial for understanding growth, decline, or change over time. The formula for percentage change is: **Percentage Change = ((New Value - Original Value) / Original Value) × 100** * If the result is positive, it's a percentage increase. * If the result is negative, it's a percentage decrease. For example, if a product's price increased from $40 to $50: * Change = $50 - $40 = $10 * Percentage Increase = ($10 / $40) × 100 = 25% If a product's price decreased from $50 to $40: * Change = $40 - $50 = -$10 * Percentage Decrease = (-$10 / $50) × 100 = -20% (or a 20% decrease) Understanding these concepts is vital for analyzing trends, whether it's sales growth, population changes, or even the performance of a portfolio. The "Data Kalimat" mentions "Commented Dec 20, 2022 at 13:05" and "Answered Mar 23, 2010 at 9:19," which can be seen as data points over time. If we were tracking the activity on a forum, we might analyze the percentage increase in comments or answers between these dates, demonstrating the dynamic application of percentage change in understanding trends and engagement over different periods. This builds directly upon the foundational understanding of "20 is what percent of 50" by introducing the element of change.Mastering Numerical Literacy: A Lifelong Skill
The journey from understanding "20 is what percent of 50" to confidently tackling complex financial statements or statistical reports is a testament to the power of foundational numerical literacy. Percentages are more than just numbers; they are tools for comparison, analysis, and informed decision-making. In an increasingly data-driven world, the ability to interpret and utilize percentages is no longer just a mathematical skill but a critical life skill. It empowers individuals to navigate personal finances, evaluate news and media critically, and contribute meaningfully in professional settings. The anecdotes from the "Data Kalimat," such as the user with a "sql server installed on a local machine... for personal projects" seeking a "free host," illustrate the continuous, practical application of problem-solving and resourcefulness in everyday scenarios. Just as one might seek a free host to manage personal projects without spending a penny, understanding percentages allows you to manage your finances, make smart purchases, and achieve your goals without unnecessary costs or misunderstandings. The seemingly "late answer, but hopefully worthwhile" sentiment applies perfectly to mastering any fundamental skill; the effort invested in truly understanding concepts like percentages will always yield worthwhile returns throughout your life. By consistently applying the principles discussed, practicing with various examples, and recognizing the omnipresence of percentages in your environment, you will not only master calculations like "20 is what percent of 50" but also cultivate a robust numerical intuition that serves you well in every aspect of life.We hope this comprehensive guide has demystified the concept of percentages and provided you with a clear understanding of how to solve problems like "20 is what percent of 50?". Do you have any other percentage puzzles you'd like us to break down, or perhaps a real-world scenario where percentages have helped you make a crucial decision? Share your thoughts and questions in the comments below! If you found this article helpful, consider sharing it with friends or colleagues who might also benefit from a clearer understanding of this essential mathematical concept. For more insights into practical mathematics and financial literacy, be sure to explore our other articles.
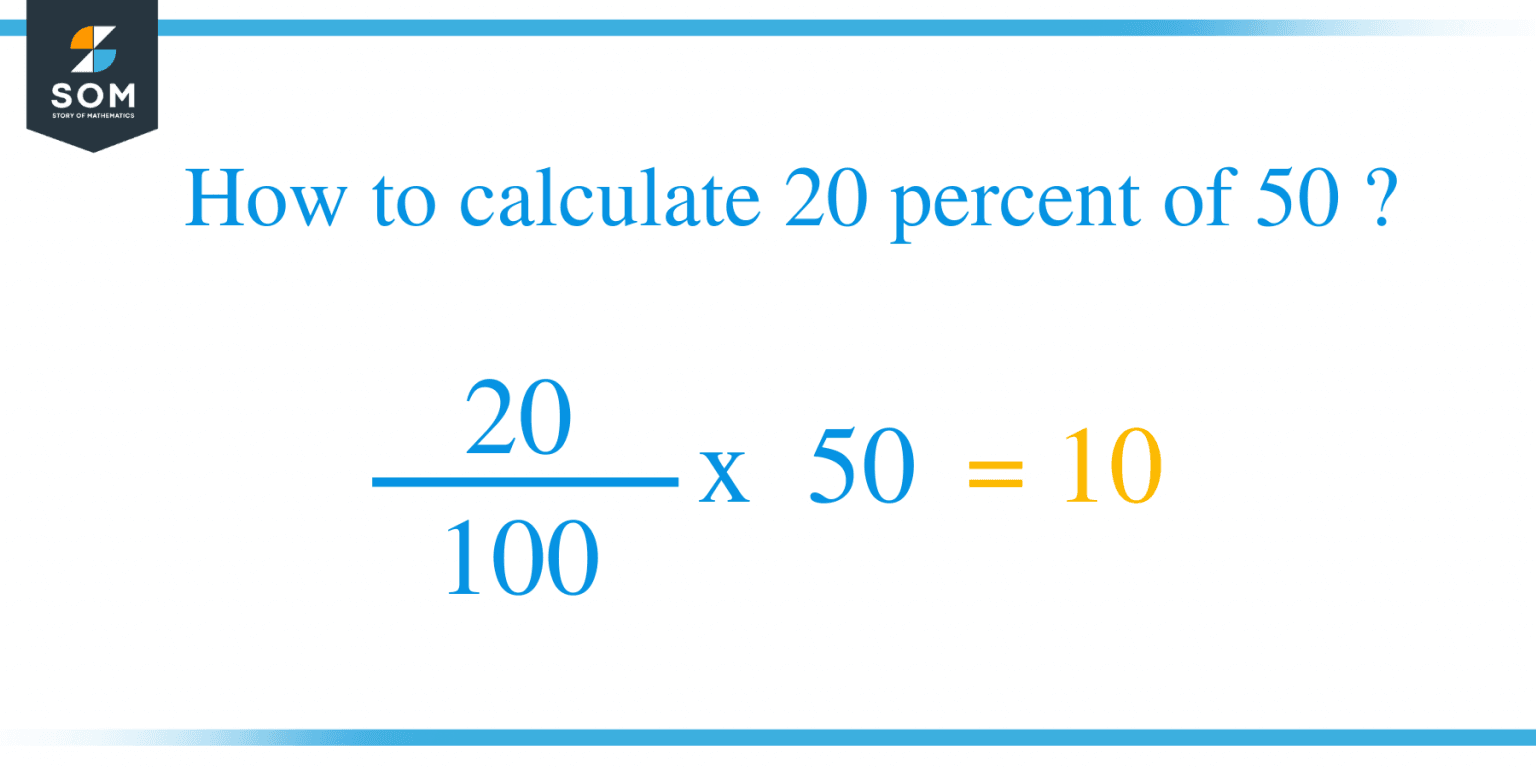
What is 20 percent of 50 + Solution With Free Steps?
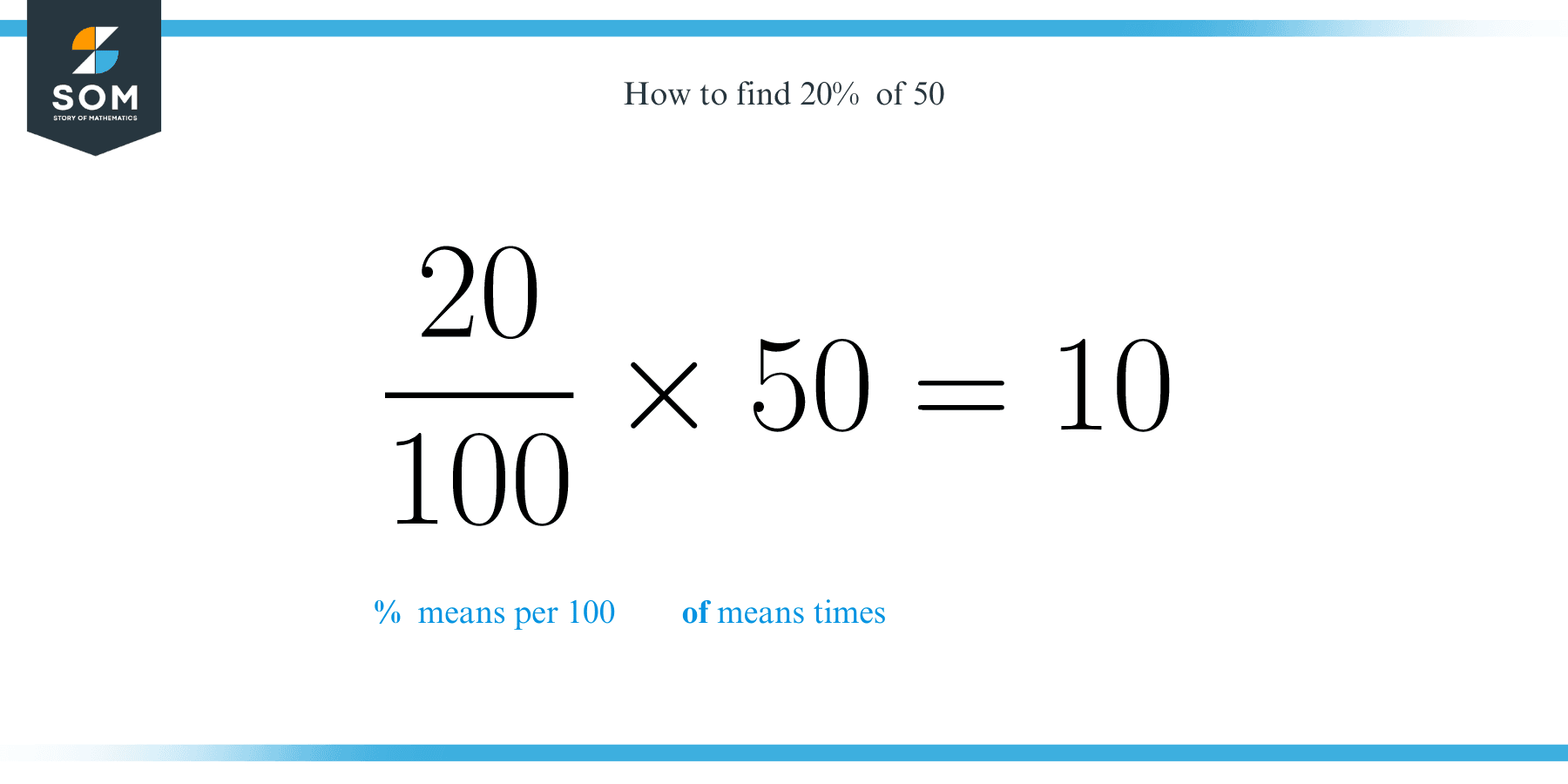
What is 20 percent of 50? - The Story of Mathematics - A History of
What Is 20 Percent Off 50? Plus Percentage Calculator